[금융전략을 위한 머신러닝] 1. 인공 신경망

아래 내용은 “금융전략을 위한 머신러닝” 책을 공부하며 정리한 내용입니다.

Chapter 03. 인공 신경망

인공 신경망은 인공 뉴런이라고 불리는 노드가 연결된 집합체로, 연산을 수행하는 시스템이다.

구조, 훈련, 하이퍼파라미터

구조

인공 뉴런

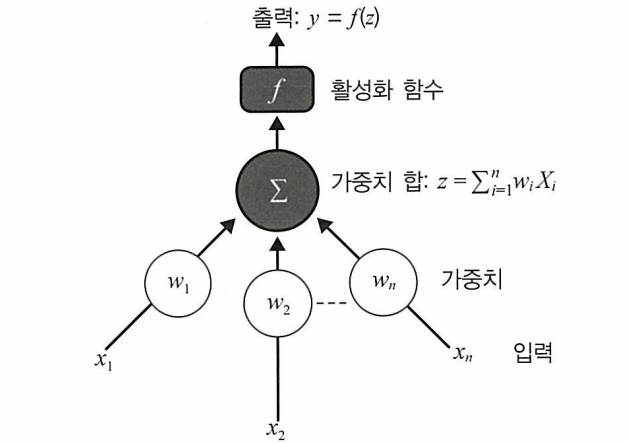
생물학적 뉴런의 작동 방식을 모방한 수학적 모델로, 입력 신호에 가중치를 적용하고 활성화 함수를 통해 출력 값을 생성한다.

신경망 구조

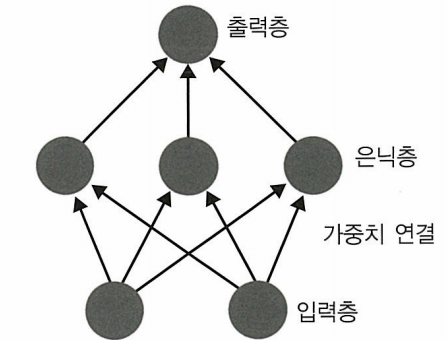
신경망 구조는 인공 뉴런들이 계층적으로 연결된 형태로, 입력층, 은닉층, 출력층으로 구성되어 복잡한 패턴 인식과 예측 작업을 수행한다.

훈련

• 순전파 : 신경망에서 입력값을 받고 예측값이라고 하는 출력을 얻는 과정

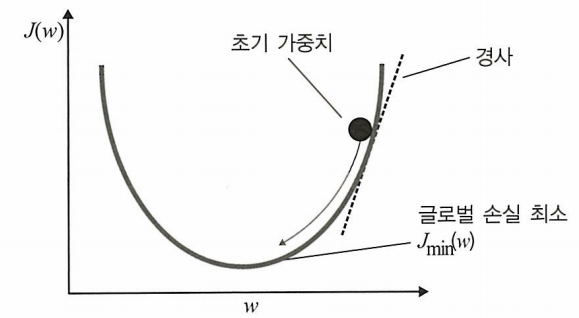
• 역전파: 훈련셋을 가지고 손실 함수를 최적화 즉 손실을 최소화 하는 것

경사 하강법

하이퍼파라미터

활성화 함수

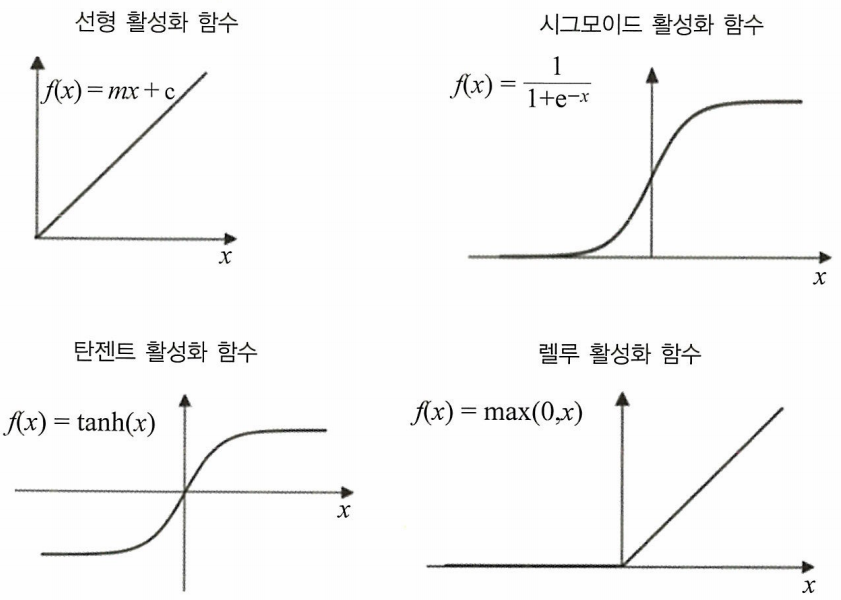
• 선형 함수: 입력에 대한 선형적인 변환을 수행하며, 수학적으로 f(x) = ax + b의 형태를 갖는다. 이 함수는 비선형성을 도입하지 않기 때문에 신경망에서 여러 층을 쌓아도 복잡한 패턴을 학습하기 어렵다.

• 시그모이드 함수: S자 형태의 곡선을 가지며, 입력 값을 0과 1 사이의 실수로 변환한다. 수학적으로 f(x) = 1 / (1 + exp(-x))로 표현되며, 이진 분류 문제에서 활성화 함수로 자주 사용된다. 그러나 큰 입력 값에서는 기울기가 거의 0에 가까워져 ‘기울기 소실’ 문제가 발생할 수 있다.

• 하이퍼볼릭 탄젠트 함수: 출력 범위가 -1에서 1 사이인 S자 형태의 함수로, 수학적으로 f(x) = tanh(x)로 나타낸다. 출력이 0을 중심으로 대칭이기 때문에 시그모이드 함수보다 학습이 빠를 수 있다. 하지만 역시 극단적인 입력 값에서 기울기 소실 문제가 발생할 수 있다.

• ReLU 함수: 입력 값이 0보다 작으면 0을 출력하고, 0보다 크면 그 값을 그대로 출력하는 함수이다. 수학적으로 f(x) = max(0, x)로 정의되며, 계산이 간단하고 깊은 신경망에서도 기울기 소실 문제가 적어 효과적이다. 다만 음의 입력에 대해 뉴런이 영구적으로 비활성화되는 ‘죽은 ReLU’ 문제가 있을 수 있다.