[파이썬으로 구현하는 로보어드바이저] 3. 딥러닝 예측을 통한 시장 모니터링
아래 내용은 “파이썬으로 구현하는 로보어드바이저” 책을 공부하며 정리한 내용입니다.
Chapter 8. 딥러닝 예측을 통한 시장 모니터링
딥러닝 예측 모델 구성
분석
딥러닝은 이미지, 자연어, 시계열 등 다양한 분야에서 우수한 성능을 보이며 주목을 받고 있다. 이 책에서는 그중에서 시장 예측에 활용될 시계열 데이터 분석에 집중한다.
시계열 분석 (time series analysis)
시계열 분석은 주가, 환율 등 경제 데이터의 변동, 기온/습도 등 기상 데이터의 변동과 같이 시간의 흐름에 따라 변화하는 데이터를 분석하는 방법이다. 시계열 분석은 주로 데이터의 경향이나 전망을 위해 사용한다.
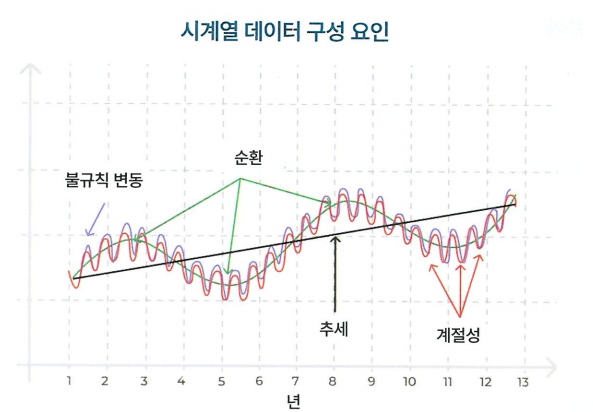
시계열 데이터는 시간에 따라 여러 요인에 의해 변동한다. 이 중 가장 일반적으로 다뤄지는 변동 요인에는 추세 변동, 계절 변동, 순환 변동 그리고 불규칙 변동이 있다.
추세 변동 (trend variation)
추세 변동은 장기적인 추세나 경향성을 나타내는 변동이다. 이는 시간의 흐름에 따라서 데이터가 일정한 경향을 따라 움직이는 것을 나타내며 경제 성장, 인구 변동 등과 관련된 요인으로 발생할 수 있다.
계절 변동 (seasonal variation)
계절 변동은 일정한 주기를 가지고 발생하는 패턴이다. 계절 변동은 주로 계절, 월 또는 요일과 같은 주기적인 요인에 의해 영향을 받는다. 예를 들어 겨울철에는 난방 비용이 증가하거나 여름철에는 에어컨 사용량이 증가하는 등 계절적인 변동이 발생할 수 있다.
순환 변동 (cyclical variation)
순환 변동은 경기 변동과 관련이 있는 변동이다. 일정한 주기를 가지고 데이터가 파동처럼 상하로 움직이는 것을 의미한다. 예를 들어 경기 침체와 회복이 반복되는 경제 사이클이나 부동산 시장의 호황과 불황이 순환 변동의 예시가 될 수 있다.
불규칙 변동 (irregular variation)
불규칙 변동은 예측하기 어려운 무작위 변동이다. 외부적인 충격이나 예측할 수 없는 요인에 의해 발생하는 변동이다. 예를 들어 자연재해, 정치적 불안정, 경제적 불확실성 등이 불규칙 변동의 예시가 될 수 있다.
시계열 분석은 이러한 변동 요인들을 고려해 데이터의 패턴과 트렌드를 모델링하고 예측을 수행한다. 이러한 불규칙적 시계열 데이터에 규칙성을 부여해 예측하기 위해 AR, MA, ARMA 등 다양한 통계적 모델이 있지만 최근에는 딥러닝을 통해서 패턴을 스스로 학습 하는것이 더 좋은 성능을 보여주고 있다.
딥러닝 모델
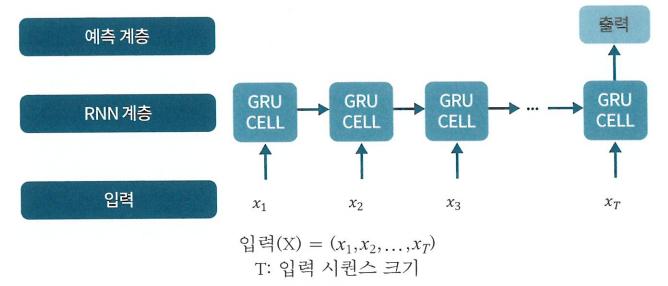
RNN 모델
RNN (Recurrent Neural Network) 모델은 순환 구조를 가지며 이전 단계의 출력을 현재 단계의 입력으로 사용하는 재귀적인 구조를 가지고 있다. 이를 통해 과거 정보를 기억하고 활용할 수 있으며, 장기적인 패턴을 학습할 수 있다. 시간에 따라 변화하는 시계열 데이터를 처리하는 데 강점을 가지고 있으나, 오류 누적 및 기울기 소실 문제 혹은 긴 시퀀스에서는 멀리 떨어진 정보를 잘 기억하지 못하는 단점이 있다. 일반적인 RNN 구조에는 LSTM (Long Short-Term Memory)과 GRU (Gated Recurrent Unit) 모델이 있다. LSTM 및 GRU 모델은 기울기 소실 문제를 완화하기 위해 설계되었다.
트랜스포머 모델
트랜스포머 (Transformer) 모델은 주로 자연어 처리에 사용되었지만 시계열 예측에도 적용될 수 있다. 트랜스포머는 셀프 어텐션 메커니즘 (Self-Attention Mechanism)을 사용해 입력 시퀀스의 전역적인 중요성을 모델링한다. 이 모델은 입력 시퀀스의 모든 위치에 대한 상대적인 중요도를 계산해 주요 패턴을 학습한다. 이를 통해 트랜스포머는 RNN과 달리 병렬 처리가 가능하며 더 긴 시퀀스를 처리하는 데 유리하다. 또한 트랜스포머는 층 (Layer) 간의 정보 전달을 위한 잔차 연결 (Residual Connection)과 층 정규화 (Layer Normalization)를 사용해 안정적인 학습을 돕는다. 그러나 모델이 무겁고 학습하는 데 시간이 오래 걸린다는 단점이 있다.
TCN 모델
TCN (Temporal Convolutional Network)은 1D 합성곱 신경망 (1D Convolutional Neural Network) 구조를 사용해 시계열 데이터를 처리한다. TCN은 고정 크기의 필터를 사용해 각 시간 단계의 지역적 패턴을 학습하며, 다음 시간 단계의 값을 예측한다. 시계열에서 긴 시간적 의존성을 캡처하는 데 RNN보다 뛰어난 성능을 보인다. 또한 TCN은 병렬 처리가 가능하고 트랜스포머 기반 방법과 비교해 학습이 빠르고 하이퍼파라미터 (Hyperparameter) 조정이 적은 장점이 있다
RNN
이 책에서는 GRU를 사용한 RNN 모델을 사용해 분석을 진행한다. GRU는 Gated Recurrent Unit의 약자로 RNN의 한 종류이다. GRU는 장기 의존성 문제 (Long-Term Dependency Problem)를 해결하기 위해 게이트 구조로 설계된 셀로, 시퀀스 데이터를 모델링하는 데 주로 사용된다. 여기서 장기 의존성 문제란 은닉층의 과거의 정보가 마지막까지 전달되지 못하는 현상을 의미한다.
GRU는 LSTM에 비해 더 간단한 구조를 가지고 있지만 비슷한 성능을 제공한다. GRU는 순차적인 데이터를 처리하면서 과거 정보를 기억하고 현재 입력과 함께 사용한다.
GRU의 핵심 아이디어는 게이트(Gate)라는 개념을 도입한 것이다. GRU는 업데이트 게이트 (Update Gate)와 리셋 게이트 (Reset Gate)라는 2가지 게이트를 사용한다.
업데이트 게이트는 현재 입력과 이전 상태를 고려해 새로운 상태를 얼마나 업데이트할지를 제어한다. 이를 통해 GRU는 중요한 정보를 유지한다.
리셋 게이트는 현재 입력과 이전 상태를 고려해 얼마나 이전 상태를 재설정할지를 결정한다. 이를 통해 GRU는 이전 상태에 대한 영향력을 줄이거나 증폭시킬 수 있다.
GRU는 LSTM보다 더 간단한 구조를 가지고 있어 계산 비용이 적고 학습 시간이 더 짧다는 장점이 있다.
SCINET
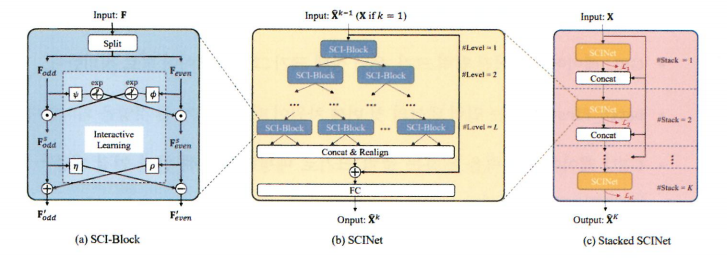
SCINet 모델은 시간의 불규칙성을 고려하기 위해 입력 데이터의 짝수(even), 홀수(odd) 스텝을 구분하는 아주 독특한 방식을 제안했다.
(a) SCI-Block의 구조
SCI-Block의 그림을 보면 실제로 짝수 스텝과 홀수 스텝으로 분할되면서 상호 간의 네트워크를 연결해 학습하는 구조를 알 수 있다. 각 짝수, 홀수 스텝의 데이터는 건블럭식 필터를 통해 시퀀스의 특성이 추출된다.
(b) 트리 구조
SCI-Block을 계층별로 쌓은 트리 구조를 나타낸다. 최종적으로 Zig-Zag 얼라인먼트를 통해 합친 후 완전히 연결돼 출력값을 도출한다. 이 구조를 (c) 그림과 같이 여러 개 쌓은 스택 형태로 구성할 수도 있다.
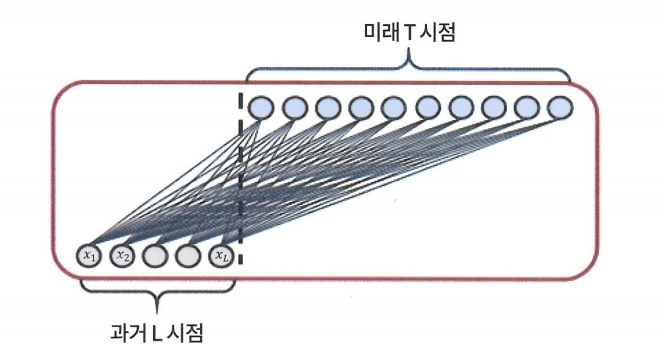
NLinear
NLinear 모델은 길이 L의 입력 시퀀스에 대해서 가장 마지막 값을 뺀 후 MLP를 통해 학습시키고 다시 그 값을 더해 실제 값이 존재하는 분포로 복귀시켜 길이 T의 시퀀스를 예측한다.
매우 간단한 구조이지만 데이터가 상승하거나 하락하는 추세를 지녔을 경우 평균 및 분산으로 데이터를 정규화하면 평가 데이터의 분포 이동이 발생할 수 있기 때문에 이러한 점을 보완한 형태라고 할 수 있다.
다시 말해서 데이터가 비정상성 (Non-Stationary)을 가져서 분포가 계속 바뀌는 경우, 분포를 간단히 표준화하는 방법으로 마지막 값을 빼고 더하는 방법을 제안했다고 할 수 있다.