[금융전략을 위한 머신러닝] 4. 비지도 학습: 차원 축소

아래 내용은 “금융전략을 위한 머신러닝” 책을 공부하며 정리한 내용입니다.

Chapter 07. 비지도 학습: 차원 축소

차원 축소 기술

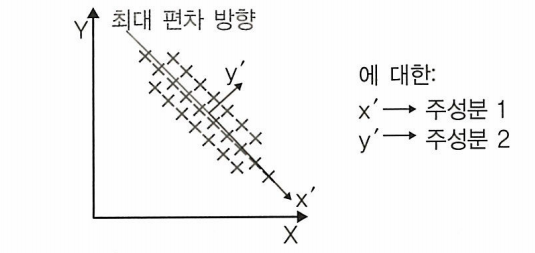
주성분 분석

주성분 분석이란 데이터의 분산을 가능한 한 많이 유지하면서 변수가 많은 데이터셋의 차원을 줄이는 것

PCA를 사용하면 원래 데이터 포인트의 대부분을 설명할 수 있는 데이터의 다른 표현이 있는지 여부를 이해할 수 있다.

주성분 분석

최대 분산을 포함하는 새로운 방향을 주성분이라고 하며, 주성분은 설계상 서로 직교한다.

주성분을 찾는 방법에는 고유 분해와 특이값 분해(SVD) 두가지 방법이 있다.

고유 분해

1. 특서에 대한 공분산 행렬을 생성
2. 공분산 행렬을 계산 후 고유 벡터를 계산 (최대 분산 방향)
3. 고윳값 생성 (주성분의 크기를 정의)

특이값 분해

행렬을 세개의 행렬로 분해 하는 것

커널 주성분 분석

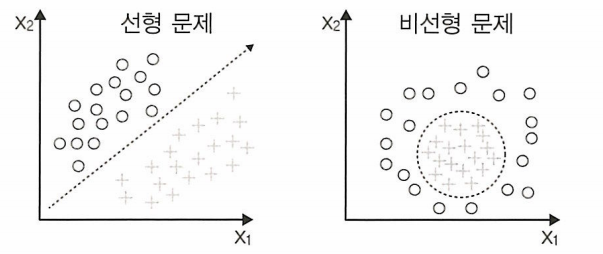
PCA의 주요 한계는 선형 변환만 가능하다는 것

커널 주성분 분석(KCPA)은 PCA를 확장하여 비선형성을 처리한다.

커널 주성분 분석

t-분산 확률적 이웃 임베딩

각 포인트 주변의 이웃 확률 분포를 모델링해 차원을 줄이는 차원 축소 알고리즘

이웃이란 주어진 포인트에서 가장 가까운 포인트 집합을 의미

알고리즘이 고차원에서 떨어져 있는 포인트 사이의 거리를 유지하는 것과 반대로 저차원에서 유사한 포인트를 함깨 유지하는 것을 강조한다.